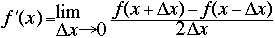
The method of finite differences relies upon making finite approximations to the conventional derivative of a continuous function. Recall that a regular derivative can be defined as:
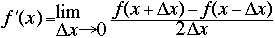
A finite derivative, on the other hand can defined several ways, the simplest of which is:
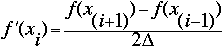 or
or
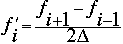
Where xi is the ith element of the matrix x representing the continuous function x. [[Delta]] is the grid spacing, or the distance between each point in x.
More complicated expressions can also be derived from similar principles, as shown by the definition below:
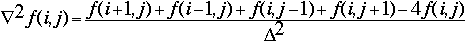
Where f is a two-dimensional function, represented as a two dimensional matrix. It is assumed in this example that the grid spacing in both directions is the same, i.e. [[Delta]]x=[[Delta]]y=[[Delta]]. This is typically a desirable property for modeling physical systems, as it simplifies most calculations. In our model, we made this assumption.